Reservoir Computing

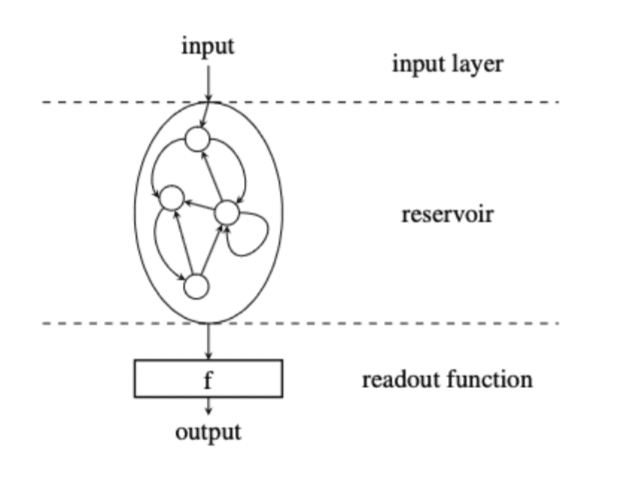
Reservoir Computing (RC) consists of a learning machine that maps input signals to a higher dimensional space through the dynamics of a fixed, non-linear reservoir; the embedding produced by the reservoir is then fed to a readout function for the final output.
In RC, the reservoir is a fixed “black box” and we learn only the readout. There are two main advantages to this:

• reducing the complexity of the learning problem, as we only need to learn the readout;
• exploiting the computational power of an off-the-shelf reservoir.

Properties

Any reservoir must satisfy two properties:

• It must be made of individual, non-linear units;
• It must be capable of storing information.

These two properties endow a reservoir with a recurrent nature, i.e., a state to store information over time, and thus solve complex problems. The power of RC stems from the fact that, in theory, any dynamical system satisfying the two properties can be used as a reservoir: even a bucket of water that performs computations given inputs that cause perturbations on its surface .

Examples

The following is a (non-exhaustive) list of instances of RC:

• Recurrent Neural Networks are the foremost instance of RC, being neural networks that display temporal dynamic behavior by processing inputs (in the form of sequences) and internal states (in the form of memory);
• Extreme Learning Machines are feed-forward neural networks consisting of n layers, where only the parameters of the output need be learned, while the other n – 1 are initialized randomly and never updated;
• Echo State Networks are recurrent neural networks where only the parameters of the output layer need be learned, whereas the (sparsely connected) hidden layer is randomly initialized and never updated;
• Liquid State Machines use as reservoirs spiking neural networks, whose neurons are randomly connected to each other (and thus have a recurrent nature), while the readout is a linear discriminator;
• Deep Reservoirs employ deep neural networks in lieu of the reservoir;
• Quantum reservoirs exploit the non-linear nature of quantum mechanical interactions and processes to form the non-linear reservoirs;
• Physical reservoirs, see next paragraph.

Physical reservoirs

There is evidence that physical bodies can operate as reservoirs . As already mentioned, inputted water ripples with electric motors and analyzed the ripples in the readout to solve a pattern recognition task. highlighted how soft bodies, given their infinite degrees of freedom, are ideal physical reservoirs and exploited the non-linear dynamics of a soft silicone arm to learn a readout that solved standard benchmarks. Physical reservoirs are relevant as they come for-free in many natural systems (e.g., robotics).

Citations